L'arbelos

L'arbelos (ou tricercle de Mohr, du nom du mathématicien danois Georg Mohr) est une figure géométrique plane étudiée, entre autres, par Archimède (–287 ; –212). Le terme "arbelos" signifie couteau du savetier.

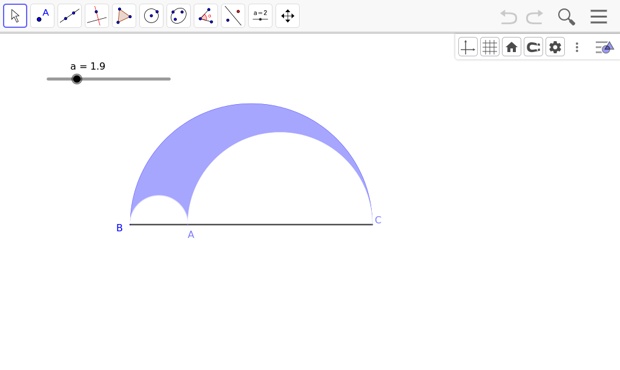
Soit \([\text{BC}]\) un segment de longueur \(8\). On considère le demi-cercle de diamètre \([\text{BC}]\).
On place un point \(\text A\) sur \([\text{BC}]\). On appelle `x` la longueur \(\text{AB}\).
\(\)On trace les deux demi-cercles de diamètres \([\text{AB}]\) et \([\text{AC}]\), inclus dans le premier demi-cercle.
On note \(\mathcal{A}\) la fonction qui donne l'aire de la partie colorée en bleu (voir figure ci-dessous) en fonction de \(x\).

Vous pouvez ci-dessous faire varier le curseur pour déplacer le point A.

1. Quelles sont les valeurs prises par \(x\) ?
2. Montrer que \(\mathcal{A}(x)=-\dfrac{\pi}{4}x^2+2\pi x\).
3. Résoudre dans \(\mathbb{R}\) l'équation \(\mathcal{A}(x)=0\). Le résultat paraît-il cohérent ?
4. Montrer que \(\mathcal{A}(x)=-\dfrac{\pi}{4}(x-4)^2+4\pi\).
5. a. Étudier les variations de \(\mathcal{A}\) sur \([~0~;~4~]\) puis sur \([~4~;~8~]\).
    b. Dresser le tableau des variations de la fonction \(\mathcal{A}\).